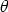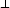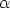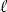The University of Sydney - School of Mathematics and Statistics

Derivation of the formula	Page 3 of 7

Unless one (or both) of the vectors is zero, it is not obvious how to get the formula to compute the vector product from the geometric definition of the vector product. If you are interested in how to obtain it, here is a possible way.

The procedure depends on looking at projections of the parallelograms spanned by the vectors u and v into the three coordinate planes. We proceed in three steps.

Step 1

We first look at vectors in the xy-plane. The magnitude of u × v is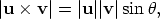

so u×v = ±(|u||v| sin 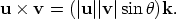)k. The sign is positive if moving u to v through the smaller angle is counterclockwise and negative in the other case. Hence if we let positive in the former and negative in the latter case we get

(We use that sin(-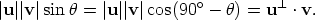) = - sin .) Now let u be the vector obtained by rotating u counterclockwise by 90°. As |u| = |u| it follows from the definition of the scalar product that

Two possible situations are shown below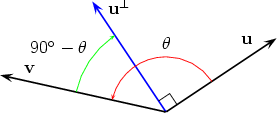

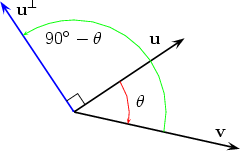
We therefore get u × v = (u· v)k.

Now assume that u = u₁i + u₂j and v = v₁i + v₂j. Then from the figure below u 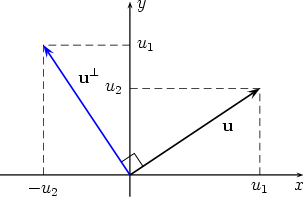= -u ₂i + u₁j.

Using the formula for the scalar product we get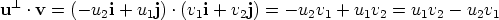

and therefore u × v = (u· v)k = (u ₁v₂ - u₂v₁)k as claimed.

Step 2

Let now u and v be two non-zero and non-parallel vectors in space. Denote by P the parallelogram they span when placed tail-to-tail. By definition of the vector product the area of P is A = |u × v|.

We now project P along the z-axis onto the xy-plane. That projection, P', is spanned by the projections u' and v' of u and v onto the xy-plane.

It will be shown in Step 3 that the area, A', of P' is given by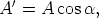

where is the acute angle between the planes containing P and P'.

Observe that is also the acute angle between the z-axis and w := u × v, which are perpendicular to the respective planes.

Writing w = w₁i + w₂j + w₃k it follows that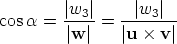

as you see from the figures below, representing a cross section along w and the z-axis.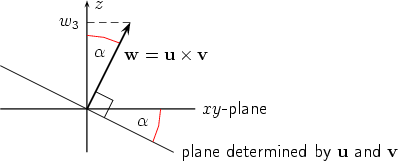

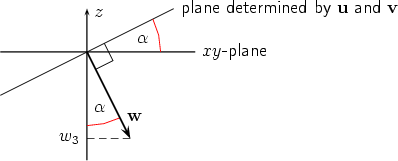
If w₃ > 0 the triple u', v', k is right handed, otherwise it is left handed. Hence by the definition of the vector product u'× v' = w₃k. If we note that u' = u₁i + u₂j and v' = v₁i + v₂j we conclude from Step 1 that w₃ = u₁v₂ - u₂v₁.

We get the other components w₁ and w₂ by the cyclic permutation i j k i. If we do so we get w₁ = u₂v₃ - u₃v₂ and w₂ = u₃v₁ - u₁v₃, proving the formula for u × v.

Step 3

We determine how the area of a parallelogram is changed when it is projected onto a plane. Suppose that E₁ and E₂ are two planes intersecting at a line 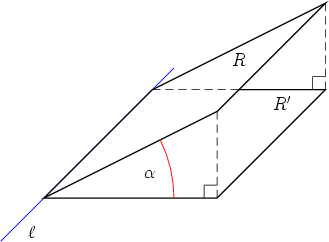. If R is a rectangle on E₂ with area A and one edge parallel to , then the area of its projection, R', orthogonal to E₁ is A cos , where is the acute angle between the two planes:

Now look at an arbitrary parallelogram P on E₂ spanned by vectors u and v. We can transform it into a rectangle of the same area such that one edge of that rectangle is parallel to 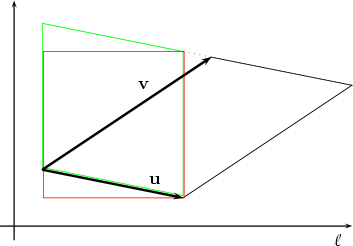as shown below

The projections of the black, green and red parallelograms into E₁ have all the same area as the picture looks very similar in E₁. Suppose the area of the original black parallelogram is A₂ and that of its projection is A₁. Then the area of the red rectangle is A₂ and that of its projection is A₁. From the previous considerations we know that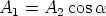

with being the acute angle between E₁ and E₂.